Python Basics Operations

Float number and bool

We cannot directly compare the float value, like using the logic “==” symbol. But we can use: the way that using the division method to compare the result with a very small value.

1
2
3

# float_num == cannot be used into the float number comparision.
abs(float_num - 12.2 < 1e-5)
# here the 1e5 means the 0.1^(-5), just equals to 0.000001.

1
2
3

Convert a number into the inverse number:
Like num = 150
We got result = 51

num = 150
digit1 = num % 10
digit2 = num // 10 % 10
digit3 = num // 100

result = digit1 * 100 + digit2 * 10 + digit3

Swap the two value’s values:

# here is the standard way
num1 = 10
num2 = 15

tmp = num2
num2 = num1
num1 = tmp

# this is to help you to exchange the variables, but if you are in python we can do:
num1, num2 = num2, num1

Google Codestyle Pygide

Enumerate

In python we can use range() or just for loops to loop the elements from a list, but we still strongly suggest we use the enumerate, since it looks more python.

1 2	for (index, num) in enumerate(nums): return (index, num)

Reverse the list!!! Using range()

for i in range(len(nums) - 1, -1, -1):
	# range(n, m, -1) n = [n, n - 1, n - 2, ..., m + 1]
	print(nums[i], end = " ")
print()

While and for

While loop is just equal to the for loop in many ways:

i = 0
while i < len(scores):
	print(score[i])
	i += 1

	# thats the biggest difference, since if in for, we do not need to add the value manually.

Swap a function to exchange the values into an array

Input = '[1, 2, 3, 4]'
index1 = '2'
index2 = '3'
Result = '[1, 2, 4, 3]'

1
2
3

def swapInteger(swapList, swapIdx1, swapIdx2):
    swapList[swapIdx1], swapList[swapIdx2] = swapList[swapIdx2], swapList[swapIdx1]
    return swapList

Class

In python the “self.” all can represent the inner nature of a function.

class Student(): # Class name should follow the camel way
	def __init__(self, name, score):
		# we defined two natures of the student: name & score
		self.name = name
		self.score = score

	# here we defined the behaviour
	def speak(self):
		print(self.name, self.score)

init

init is the default construnction function that will run when you create that class. This is the compulsory element of the class.

self

Self it is the object itself, when we define the class we must declare it, but when we call it we will not see.

From class to object

Instance is just object.

student = Student('Jack', 90)
# we can visit the value of that object
student.name
student.score
# call the function from that class object
student.speak()
# reset the value
student.name = 80

Existence

We need to have the existence judge before we really run the function:

It can combine two cases: 1) End Case 2) Base Case.

1
2
3

# here is the base case
if root is None:
    return

List CRUD

Create

1	list = list_1 + list_2

1 2	list = list * 3 # It will duplicate all the elements in the list three times

Read

iteration

1 2	for x in list_a: print(x, end = " ")

index id

list_a[n]

slice

list_a[:]

1 2	2 in list_a # it will return a boolean value

index method

list_a.index("the value you want to search")

# it will tell you the index of the value you search, if not in there will be invalid
if 2 in list_a:
    return list_a.index(2)
# in order to prevent that if we cannot find the index value and output the bug issues, we need to firstly have a if then if true, we then print the index of that value, else just do not.

count

1 2	list.count(2) # count is to get how many frequencies that value occurred from the list

Update

update through the index

1	list_a[2] = ...

Update through slicing

1	list_b[:n] = [,,,]

append

1	list.append("will add an element from the end of the list")

insert

1 2	list.insert(index, "the element you want to insert") list.insert(2, "the element you want to insert")

extend

1
2
3

list_a = ["1", "2", "3"]
list_b = ["a", "b", "c"]
list_a.extend(list_b)

This will enable us to insert the values before the list we want to append. It looks like “+”, but for “+”, we need to generate a new list, but for this strategy, there is no need to do this.

1	list_b = ["1", "2", "3", "a", "b", "c"]

Delete

1 2	list_b [:2] = [] # delete all the values before the list_b[2]

pop

1
2
3

list_b.pop(index)
list_b.pop(2)
# this will delete the list_b[2]

If there is no index, it will defaultly delete the final value.

remove

1
2
3

list_b.remove(index_value)
list_b.pop("A")
# this will remove the value from the list

del

1
2
3

del list_a[3]
# we can use delete to delete the value by index or by slicing
del list_a[:n]

is_empty

if self.items：
	# if the list is empty it will return false, if not empty, it will be True.

if not self.items:
    # if the list is empty it will return True, if not, it will be False.

Others

len

1	len(list_a)

sort

1 2	list_a.sort() # it will generate a sorted version of the list_a

reverse

1 2	list_a.reverse() # it will reverse the list

reverse sort

1 2	list_a.sort(reverse = True) # it will reverse from the big elements downto the small ones

List Generator

1 2	list_demo = [i for i in range(101) if i % 5 == 0] # we can easily generate the list by this way.

# generate a multiple value list
[0 for i in range(3)]
we can generate the multiple values there:
[0, 0, 0]

Tuple

We only can read tuple cannot do the CUD there.

Reference

When we do the copy the value

String CRUD

Create

1	string_a = string_a + string_b

1	string_a = string_a * 3

for

1 2	for c in string_a: print(c, end = " ")

Read

find

1 2	string_a.find("a") # we can get the index of the string value

Update

replace

1 2	string_a.replace("h", "www") # we can replace the value "h" into "www"

Delete

replace

1 2	string_a.replace("h", " ") # we can replace the value "h" into " ", by this way we can delete the "h" element.

Others

len

1	len(string_a)

format

1	"I am {}".format("Xiao")

str()

1 2	str(100) # we can invert the numerical number into a string

format the elements of the list into the string value

list_demo = ["xiao", "zhang"]

result = ""
for s in list_demo:
    result += s + " "
# here is a more elegant way
result = " ".join(list_demo)
    
# the result will be "xiao zhang"

reverse the string

# using for loop but it is not suggested!!!
s = "xiaozhang"
result = ""
for i in range(len(s)-1, -1, -1):
    result = s[i]
print(result)


# we can just using the slicing
print(s[::-1]

LinkedList CRUD

Linked list is not in the Python default data type, so we have to self define it. The first node and its reference can represent the whole linked list, because you can find from one to infinity one by one.

class ListNode:
    def __init__(self, val):
        self.val = val
        '''
        val in here is the node value, it can be integer or anything, "next" is to connect this node to 			next node.
        
        none in python is an global object, if we cannot define that value specifically, we just denote it 			as none. Since we do not want to pass no value to that variable. 
        '''
        self.next = None

def build_linkedlist():
    node_1 = ListNode(1)
    node_2 = ListNode(3)
    node_3 = ListNode(5)    
    node_4 = ListNode(7)   
    
    
    
    node_1.next = node_2
    node_2.next = node_3
    node_3.next = node_4
    
    return node_1

'''            
                Val
 * *           * *  next     * *            * *                                    
* 1 * -> None * 3 * -> None * 5 *  -> None * 7 * -> None                          
 * *           * *           * *            * *                     
  ^             ^             ^              ^
node_1        node_2         node_3        node_4
  
'''

while loop to read through the linked list

while cur is not None:
    print(cur.val, end=" ")
    cur = cur.next
print("\n")

The core idea is that if we can know the head of the linkedlist, then we can know the all linkedlist. So in most cases, we will only store the head of the linkedlist. We will make use of the head of the linkedlist, to do the CRUD for all the linkedList. And these are the core idea for the Linkedlist. We believe if we can know the head of the LinkedList, then we can know all the LinkedList.

So here, we will do the all the operations based on the manipulation of the head of the linkedlist.

Create

add(location, val)

# here we want to do the operation like: add(2, 2)
# which means we want to add a value into the location[2], and assign that value into 2

Like here: 1 > 3 > 5 > 7
The result should be: 1 > 3 > 2 > 5 > 7
"""
The logic is we have to know the:
1) the node we add (new_node) before that node, here is "3", we call it "prev", we then cut that node's connection with the next one.
2) link the new_node with the position after it (new_node.next).
3)
"""
# we cut the connection between the original node and the node after it.
new_node.next = pre.next
# we reconnect with the original node with current node we want to add.
pre.next = new_node

Here are the actual code:

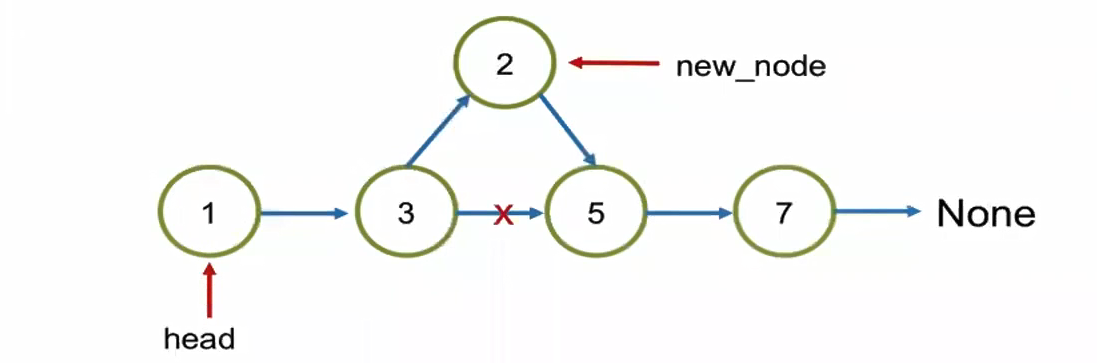
# Case 1. Add the value in within the linkedlist, which means the location is > 0
    def add(self, location, val):
        if location > 0:
            # if we want to insert the location in 2, then the position before it should be "1". If from head to the position of "1", we need to let the head to go 1 step only, if 3 then 2 steps.
            # initiate the head node
            pre = self.head
			for i in range(location - 1):
                # here it means to go forward 1 step
                pre = pre.next
            # find out the value of the new node
			new_node = ListNode(val)
            # disconnect and reconnect
            new_node.next = pre.next
            pre.next = new_node

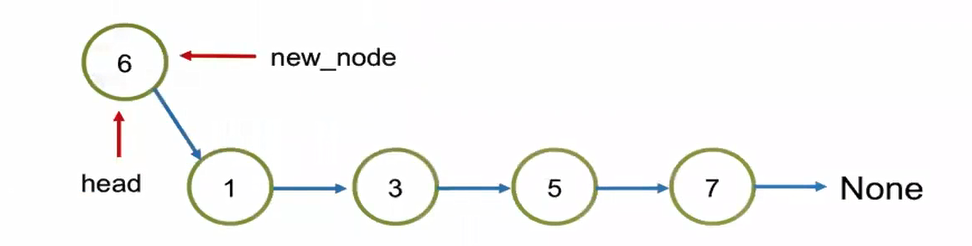
# Case 2. Add the value in the head, where the location is 0
		elif location == 0:
        	new_node = ListNode(val)
            new_node.next = self.head
            self.head = new_node

Read

get(location)

Here, we need to do get(2)

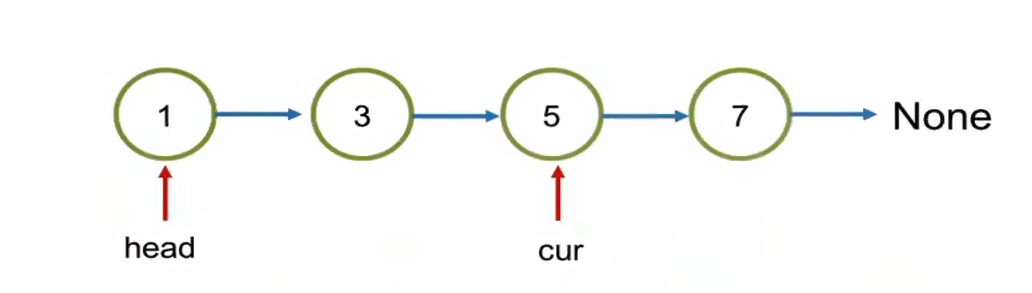
def get(self, location):
    # initiate the header value as cur
    cur = self.head
    for i in range(location):
        cur = cur.next
    return cur.val

traverse()

def traverse(self):
    cur = self.head
    while cur is not None:
        print(cur.val, end = " ")
       	cur = cur.next
   	print()

is_empty()

Check whether it is an empty linkedlist:

1 2	def is_empty(self): return self.head is None

Update

set(location, val)

The set() function is very similar to the get function, but the get() is only return the value instead of get change the value.

def set(self, location, val):
    cur = self.head
    for i in range(location):
        cur = cur.next
    cur.val = val

Delete

remove(location, val)

Remove() is very similar to the add() operations.

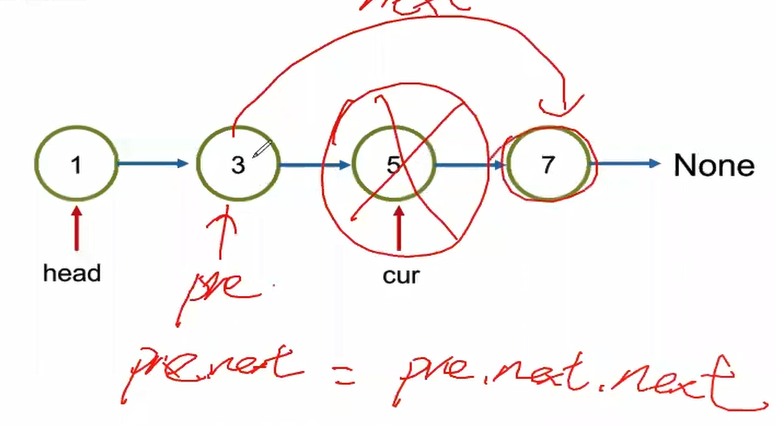
If we want to remove the node we want to remove, we should remove the node before that node.

# Case 1. Remove the value in within the linkedlist, which means the location is > 0
def remove(self, location):
    if location > 0:
        pre = self.head
        for i in range(location - 1):
            pre = pre.next
       	
        pre.next = pre.next.next
    # Case 2. Remove the value in the head, where the location is 0
	elif location == 0:
        self.head = self.head.next

Stack CRUD

Stack is LIFO(last in first out).

In python, we can use list as a stack. The last element of the list can be the top stack.

List can be a kind of stack but in a higher level, since we can do the CRUD in the place we want but stack cannot. We can use the stack to realize the stack functions.

Create

push(val)

class MyStack:
    def __init__(self):
        self.items = []
        
    def push(self, item):
        self.items.append(item)

# we can just push a element there.
if __name__ == "__main__":
    my_stack = MyStack()
    for i in range(50):
        my_stack.push(i)

Read

peek(): return the top stack value which is the last value in the list.

class MyStack:
    def __init__(self):
        self.items = []
    
    def is_empty(self):
        # if empty, it will just return TRUE, if not empty then it is FALSE, this is from the python initial feature.
        return not self.items
    
    
    def peek(self, item):
        if not self.is_empty():
            return self.items[-1]
        

# we can just push a element there.
if __name__ == "__main__":
    my_stack = MyStack()
    while not my_stack.is_empty():
		my_stack.peek

Delete

pop()

It will only delete the element at the top of the stack.

class MyStack:
    def __init__(self):
        self.items = []
        
    def pop(self, item):
        return self.items.pop()

# we can just delete the last element of the list and return it.
if __name__ == "__main__":
    my_stack = MyStack()
    while not my_stack.is_empty():
         my_stack.pop()

Queue CURD

Queue is first in first out (FIFO). We can use the LinkedList to make this work. The reason that we are using the linked list instead of list is that: if we are using the list, for the head of that list, if we want to delete that node, the time complexity is o(n).

Create

enqueue(val)

Get the value into the quene.

Delete

dequeue()

remove from the queue.

size()

check the elements number within the quene.

is_empty:

Check whether the quene is empty.

Tree

The binary tree only accepts the two child node for each parent node. If there is no specification, we will think that the tree is the binary tree. Binary tree is just like linked list, it is very important data structures. And there is also some therorums, that each tree can be converted into the many binary trees.

Create

We can create a binary tree in this way:

We need to define the class of the tree:

class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left = None
        # there are only two child nodes under each node. But for linked list, we only gonna have one child node.
        self.right = None

Now, its time to build a binary tree:

def build_tree():
    node_1 = TreeNode(8)
    node_2 = TreeNode(2)
    node_3 = TreeNode(10)
    node_4 = TreeNode(1)
    node_5 = TreeNode(7)
    
    node_1.left = node_2
    node_1.right = node_3
    
    node_2.left = node_4
    node_4.right = node_5
    node_6 = TreeNode(14)

This pic shows we already defined those nodes.

node_1.left = node_2
node_1.right = node_3

node_2.left = node_4
node_2.right = node_5

node_3.right = node_6
# we finally return the root node.
return node_1

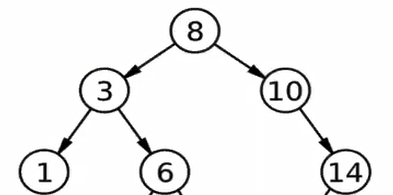
Read

We can read that data structure by traverse all the binary tree data.

DFS (Deep)

Pre-order ( root - left - right)

The logic in here is that: for each node, we firstly find the root node, then the left-sub tree, finally the right-sub tree. We call this pre-order traverse.

Now we only knew the root node, we can print the whole tree by the root node. We can print the left-sub tree, and then the right-sub tree. In this way, we can print all the trees at the same time.

def traverse_tree(root):
    if root is None:
        return 
	# if we do not specify the " ", then it can be just "/n"
    print(root.val, end = " ")
    # traverse all the left-sub tree nodes
    traverse_tree(root.left)
    # traverse all the right-sub tree nodes
    traverse_tree(root.right) # traversal

The inorder way is: left-root-right, the postorder is left-right-root.

def inorder_traverse(root):
    if root is None:
        return 
    # traverse all the left-sub tree nodes
    inorder_traverse(root.left)
    # if we do not specify the " ", then it can be just "/n"
    print(root.val, end = " ")
    # traverse all the right-sub tree nodes
    traverse_tree(root.right) # traversal

def postorder_traverse(root):
    if root is None:
        return 
    # traverse all the left-sub tree nodes
    inorder_traverse(root.left)
    # traverse all the right-sub tree nodes
    traverse_tree(root.right) # traversal
    # if we do not specify the " ", then it can be just "/n"
    print(root.val, end = " ")

BFS (Breadth First Search)

It will traverse all the tree level by level. For BFS, we will use the queue as basic data structures.

from queue import Queue
def breadth_first_traverse(root):
    if not root:
        return 
	
    que = Queue(maxsize = 0)
    # put the root node into the queue
    que.put(root)
    
    while not que.empty():
        cur = que.get()
        print(cur.val, end = " ")
        if cur.left:
            que.put(cur.left)
        if cur.right:
            que.put(cur.right)
        print()

Set

Recursive

Recursion is just a way that how we write the algorithm. Recursive is a very smart way to do the algorithm, but recursive is not compulsory. Recursive is just a way that we do the programming, any recursive problem can be divided into the non-recursive problem.

There are three important factors that we need the recursive:

the definition of the recursive

We need to know if this problem can be elegantly used the recursive way to solve.

the end case of the recursive

We should know when the recursion will be stopped.

the division of the recursive

If the recursion is not stopped, how we divide the problems?

Eg: Fibonacci，

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

0+1 = 1
1+1 = 2
2+3 = 5

The question is that if I gave you a number that in the Fibonacci, you should return the order value of that nth value.

# The definition of the recursion: F(n) = F(n-1) + F(n-2)
# The exit of the recursion: when n=1, n=2 (1th, 2th...)
# The division of the recursion: self.fibonacci(n-1) + self.fibonacci(n-1)


# this is not a good solution but good to express the recursion!!!
class Solution:
    # because this is defined within the class, if we did not add the self, the class will not find it.
    def fibonacci(self, n):
        if n == 1:
            return 0
        if n == 2:
            return 1
        
        return self.fibonacci(n-1) + self.fibonacci(n-2)

Algorithms and Data Structures:

Algorithm is the way how we do things, the data structure is is the structure of how we storage the data.

二分法

二叉树/链表

递归/DFS

BFS/拓扑排序

哈希表

双指针

动态规划

堆

Hash Table

Binary Search Tree

Binary Search

Dynamic Search

Topological Sorting

Others

Heap

Divide & Conquer

Greedy

Minimum Spanning Tree

Trie

Union Find

Time complexity expresses the efficiency of that algorithm’s efficiency.

Dynamic Programming

Linked List

Recursion

Binary Tree

Binary Search

Depth First Search (DFS)

Two Pointers

There are three kinds of two pointers:

Two pointers with the opposite direction (judge whether a string list is a palindrome)

Reverse

Reverse the string list

Judge whether the valid palindrome

From the two sides to compare.

Two Sum

Sum of two numbers

Sum of three numbers

Partition

Fast sorting

Color sorting

Two pointers with the back direction (the longest reverse list)

Two pointers with the same direction

No. 56 Two Sums

Return the value

1. Two Pointers

class Solution:
    def twoSum(self, numbers, target):
        [6, 4, 2, 9] target = 10
        
        
        # first step is to sort
        [2, 4, 6, 9]
         ^	      ^
       	 L		  R
        # next step is to find the relationship between:
        numbers[L] + nums[R] ? target
        2 + 9 = 11 > 10
        '''
        So we can know the maximum sum is like 11, and it is useless, so remove it.
        
        '''
        # we then move to the next step
        [2, 4, 6]
         ^	   ^
       	 L	   R
        
        2 + 6 =8 < 10
        '''
        So now we know that 2 is to small, even we add the largest number but still 		not meet the requirement, so we need to move it and let the L pointer into 4.
        
        '''
        [4, 6]
         ^  ^
       	 L  R
        # And [4, 6] is the exact answer

Here is the general answer, add the max value and the min value,

if > target, we just remove the max value,

if < target, we just remove the min value,

if = target, we just return true.

if we cannot even find any answer, return [-1, -1]

class Solution:
    def twoSum(self, numbers, target):
        # nlog(n)
        numbers.sort()
        # o(n)
        left, right = 0, len(numbers) - 1
        while left < right:
            if numbers[left] + numbers[right] > target:
                right -= 1
            elif numbers[left] + numbers[right] < target:
                left += 1
            else:
                return numbers[left], numbers[right]
        return [-1, -1]

Return the index

Way 1 Hashmap

class Solution:
    def twoSum(self, numbers, target):
        # now we initiate a hashtable
        hashset = set()
        # O(n)
        for number in numbers:
            # [2,4,5], target = 8
            if target - number in hashset:
                return number, target-number
            hashset.add(number)
        return [-1, -1]

Way 2 Two Pointers

If we want to return the index of the values, so we have better to use the hash map.

class Solution:
    def twoSum(self, nums, target):
        # here is like if there is no numbers, then should return the default values.
        if not nums:
            return [-1, -1]
        
        nums = [(nums, index)
               for index, nums in enumerate(nums)]
        
        """
        the codes there equals to:
        nums = [] 
        for index, numbers in enumerate(numbers):
        	nums.append((numbers, index))
        	numbers[0], 0
        	numbers[1], 1
        	numbers[2], 2
        	...
        	numbers[n], n
        """
        # now we still sort the values of the tuples
        nums.sort()
        # we only need to add the index values there
        left, right = 0, len(nums) -1 
        while left < right:
            if nums[left][0] + nums[right][0] > target:
                right -= 1
            elif nums[left][0] + nums[right][0] < target:
                left += 1
            else:
                return sorted([nums[left][1], nums[right][1]])
        return [-1, -1]

Sorting

Quicksort

There has a sequence like

Easy Understand Version

Pivot:

L > Pivot && R < Pivot => swap L and R

L <= Pivot => L = L + 1

R >= Pivot => R = R - 1

L > R => swap L and R

1
2
3

    R             Pivot             L
               
swap L and R

1
2
3

   L             Pivot 
               
L = L + 1

1
2
3

                 Pivot              R     
               
R = R - 1

1
2
3

    R                                L                  Pivot   
               
swap L and Pivot

def quick_sort(sequence):
    length = len(sequence)
    if length <= 1:
        return sequence
    else:
        # here we choosed the finial element as the pivot
        pivot = sequence.pop()
    
    
    items_greater = []
    items_lower = []
    
    for item in sequence:
        if item > pivot:
            items_greater.append(item)
        else:
            items_lower.append(item)
    return quick_sort(items_greater) + [pivot] + quick_sort(items_lower)
    
sequence = [3, 4, 6, 8, 1, 1]

print(quick_sort(sequence))
[8, 6, 4, 3, 1, 1]

def quicksort(xs):
    """Given indexable and slicable iterable, return a sorted list"""
    if xs: # if given list (or tuple) with one ordered item or more: 
        pivot = xs[0]
        # below will be less than:
        below = [i for i in xs[1:] if i < pivot] 
        # above will be greater than or equal to:
        above = [i for i in xs[1:] if i >= pivot]
        return quicksort(below) + [pivot] + quicksort(above)
    else: 
        return xs # empty lists

def quickSort(array):
    quickSortHelper(array, 0, len(array) - 1)
    return array



def quickSortHelper(array, startIdx, endIdx):
    if startIdx >= endIdx:
        return
    pivotIdx = startIdx
    leftIdx = startIdx + 1
    rightIdx = endIdx
    
    
    while leftIdx <= rightIdx:
        if array[leftIdx] > array[pivotIdx] and array[rightIdx] < array[pivotIdx]:
            (array[leftIdx], array[rightIdx]) = (array[rightIdx], array[leftIdx])
        if array[leftIdx] <= array[pivotIdx]:
            leftIdx += 1
        if array[leftIdx] >= array[pivotIdx]:
            rightIdx -= 1
    (array[pivotIdx], array[rightIdx]) = (array[rightIdx], array[pivotIdx])

Merge Sort

1	Given [3, 2, 1, 4, 5], return [1, 2, 3, 4, 5]

Binary Search (mostly already sorted)

Binary search is mostly used for search one target value from a sorted array. Binary search used some “decrease and conquer” algorithmic paradigm, which is not include “divide and conquer” algorithm.

The difference between the “permutation” and “combination” is that, for the processed data the combination is without any order!!!

Eg. from 5 numbers we just choose 3, unordered, then we call it combination:

Like (1, 2, 3) and (2, 1, 3) and (3, 1, 2) they are just the same.

The idea of the binary search is to keep the half of the “useful” data, and throw the “useless” part.

Template:

start + 1 < end
start + (end - start) / 2
A[mid] ==, <, >
A[start] A[end] ? target

Classic Binary Search Problem: https://www.lintcode.com/problem/457/

Find any position of a target number in a sorted array. Return -1 if target does not exist.

1 2	Input: nums = [1,2,2,4,5,5], target = 2 Output: 1 or 2

def binarySearch(nums, target):
    if not nums:
        return -1
    
    start, end = 0, len(nums) - 1
    
# this is the recommendation type, we can write start < end, we strongly suggest 	this type, because it is suitable for all!!!
    while start + 1 < end:
# caculate the mid point, the single "/" means just divide which has the float part, but "//" means we can only keep the integer part.
        mid = (start + end)//2
        # We need to choose these situation case by case.
        if nums[mid] < target:
            start = mid
        elif nums[mid] == target:
            end = mid
        else:
            end = mid
    if nums[start] == target:
        return start
    if nums[end] == target:
        return end
    return -1

Recursion

Find the sum of from the 1~100

BFS (Broad First Search) focuses on the width of the search.
DFS (Deep First Search) focuses on the depth of the search.

sum = 0

for i in range(101):
	sum += 1

After we use the recursion, f(1) = 1, f(n) = f(n-1) + n

1: f(1) = 1
2: f(2) = f(1) + 1

If we want to prove f(n), we need firstly prove f(1) is valid, and the next step is just to make a hypothesis that the f(n-1) is also valid. So from f(n-1) we can prove the f(n) is valid.

def recursive_sum(n):
	
	# S1. this is to prove that f(1) = 1
	if n== 1:
		return 1
	else:
		# S2. this is to prove that the f(n-1) is also valid, write the code like f(n) = f(n-1) + n
		return recursive_sum(n-1) + n

if n = 5:
	recursive_sum(4) + 5
		 recursive_sum(3) + 4 + 5
		 	recursive_sum(2) + 3 + 4 + 5
		 		recursive_sum(1) + 2 + 3 + 4 + 5
		 			1 + 2 + 3 + 4 + 5

Letter Combinations of a Phone Number:https://leetcode.com/problems/letter-combinations-of-a-phone-number/

Easy way to understand:

Example 1:

Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]
Example 2:

Input: digits = ""
Output: []
Example 3:

Input: digits = "2"
Output: ["a","b","c"]

KEYBOARD = {
        "2": "abc",
        "3": "def",
        "4": "ghi",
        "5": "jkl",
        "6": "mno",
        "7": "pqrs",
        "8": "tuv",
        "9": "wxyz"}


class Solution:
    def letterCombinations(self, digits):
        if len(digits) == 0:
            return []
        elif len(digits) == 1:
            return list(KEYBOARD[digits[0]])
        else:
            previous_list = self.letterCombinations(digits[:-1])
            last_list = list(KEYBOARD[digits[-1]])
            res = []
            for i in last_list:
                for j in previous_list:
                    res.append(j+i)
            return res

# when we do the recursion, the first step is to build a variable, here we defined a dict, which shows the mapping structure. We do not use the "0" and "1". Actually in python, the dict can be thought as the hashmap.
KEYBOARD = { 
        "2": "abc",
        "3": "def",
        "4": "ghi",
        "5": "jkl",
        "6": "mno",
        "7": "pqrs",
        "8": "tuv",
        "9": "wxyz"
}


def letterCombinations(self, digits):
    if len(digits) == 0:
        return []
    combinations = []
    # digits just the input string
    # 0 is the the index which is the starting point:0, 
    # [] is the path that if nothing in there so it is an empty list. Since here we did not read through, so it is empty.
    # combinations are the answer, if there is an anwer, we just put it in there.
    self.dfs(digits, 0, [], combinations)
    return combinations


# dfs is the core of this program.
def dfs(self, digits, index, combination, combinations):
    # the index here means which element we will do the process
    # combination means the characters it contains in the current path
    # combinations is the final result
    if index == len(digits):
        combination.append(''.join(combination))
        return 
    
    for letter in KEYBOARD[digits[index]]:
        combination.append(letter)
        self.dfs(digits, index + 1, combination, combinations)
        combination.pop()

combinationsHere are just a example of how the dfs works:

def dfs(self, "23", 0, combination, combinations):
	for letter in KEYBOARD(["23"][0]):
	=: 
	for letter in KEYBOARD(["2"]):
	=:
	for letter in "abc":
		combination.append(letter)
		NOW we got: combination = [a, b, c]
		self.dfs("23", 1, [a, b, c], combinations)

References:

https://leetcode.com/problems/letter-combinations-of-a-phone-number/discuss/1212983/python-dfs-easy-to-understand-solution

class Solution(object):
    def letterCombinations(self, digits):
        """
        :type digits: str
        :rtype: List[str]
        """
       
        combinations = []
        if not digits:
            return combinations 
        
        self.dfs(digits, 0, "",combinations)
        return combinations 
    
    def dfs(self, digits, index, combination, combinations):
        keyboard = ["","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"]
        if index == len(digits):
            combinations.append(combination)
            return;
            
        digit = int(digits[index])
        
        for i in range(0,len(keyboard[digit])):
            self.dfs(digits, index+1, combination+ keyboard[digit][i],combinations)

strStr:

source = "abcdefg"
target = "abc"


def strStr(source, target):
	if not target:
		return 0

	for i in range(len(source)):
		if source[i: i + len(target)] == target:
			return i
	return -1

print(strStr(source, target))

Much better solution:

source = "abcdefg"
target = "abc"


def strStr(source, target):
	if not target:
		return 0

	for i in range(len(source)):
		for j in range(len(target)):
			if source[i+j] != target[j]:
				break
		else:
			return i

Tips:

No many loops, no more than 3 levels:
Always ask if there is the code review part
Improvements:

**A good readable code is the most important part of the coding part, since nobody want to maintain an unreadable code there! **

if (grid[i][j]) == 1) {
	...
} else if (grid[i][j] == 2){
	...
}

Needs to explain what is Magic number: 1 & 2! There is a good way to write it shows the industrial experience:

class GridType:
	WALL = 1
	PEOPLE = 2


if (grid[i][j]) == GridType.WALL) {
	...
} else if (grid[i][j] == GridType.PEOPLE){
	...
}

The problem of the Index

1
2
3

list[i]
Since there is no limitation of the i:
We alreadys need to care about the range of i

Always decouple the codes and decrease the readability difficulty, system is much important than details. So if we use smaller modules rather than big chunks of code, that is very important. If there is an error, so it will only affect that single module instead of others.
Good naming functions:

1	find_name_by_...

Good codes do not need comments, but you can read easily from the name of the function, logic of the functions… Trash codes need comments…
Judge ways:

1
2
3

Logicality

Code Quality

Always code before ask the requirements, when totally understood, just stop chatting and write codes. Do not need to ask a lot when do the codings there. In order to save time.
If the question you already met, then you should tell the people, so he can change the question.

Introspective task: Ask a question, and answer what they feel about the question.

Triangulation: use multiple methods to do the research.

Paradigm: A typical example of a phenomenon.

Action research: Know the effective of a devices, tested by a bunch of users

Deliberate actions: Give the candy, read a book. Intions to let someone do something.

Uncontrived: Not artifical

Maintainning relationships and trust participants: Will you keep the codes/data in your own computer?